Maple Conference 2022
A Demonstration of the Maple package tensorAddOns by Jason M. Osborne.
For additional technical detail please see the post tensorAddOns.
Last Updated: Monday, October 31, 2022 - 16:46:24.
The Goal: In Maple As On Paper


Figure 1: (left) Matrix Multiplication in Tensor Notation (right) New tensorAddOns Functionality CreateTensor, DescribeTensor, and MatrixView (Note: prod is existing, but deprecated, functionality of the package tensor)
What is… A Tensor

Figure 2: Think of a Tensor as a Storage Mechanism for Higher Dimensional Data
The Process: Maple Computations Then (Transport) Visualization

Figure 3: (left) Correct Maple Computations are the Most Important (right) Export Maple Output for Application and Visualization
Math Motivation and Coding Philosophy: Gauss to Riemann Curvature
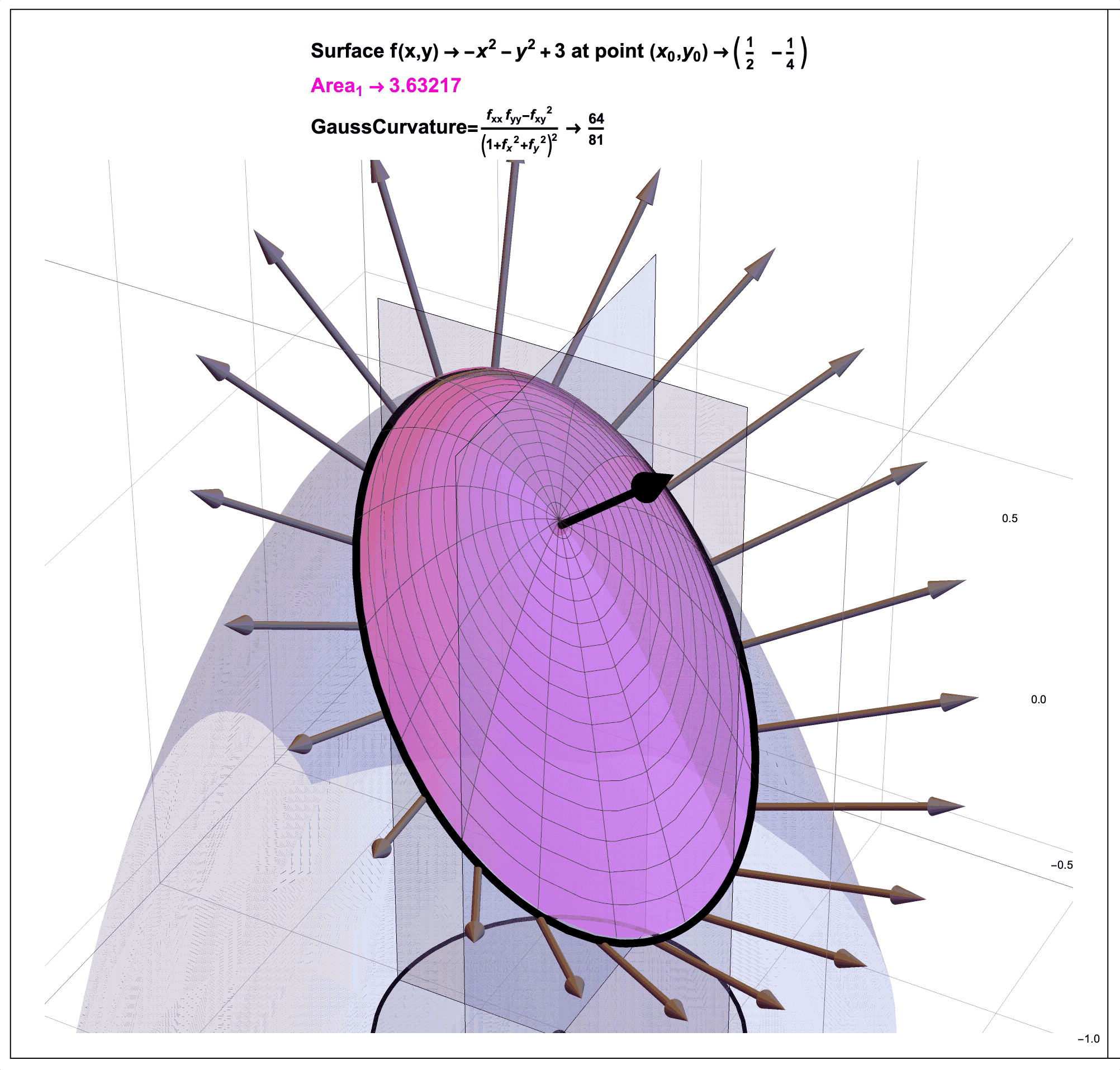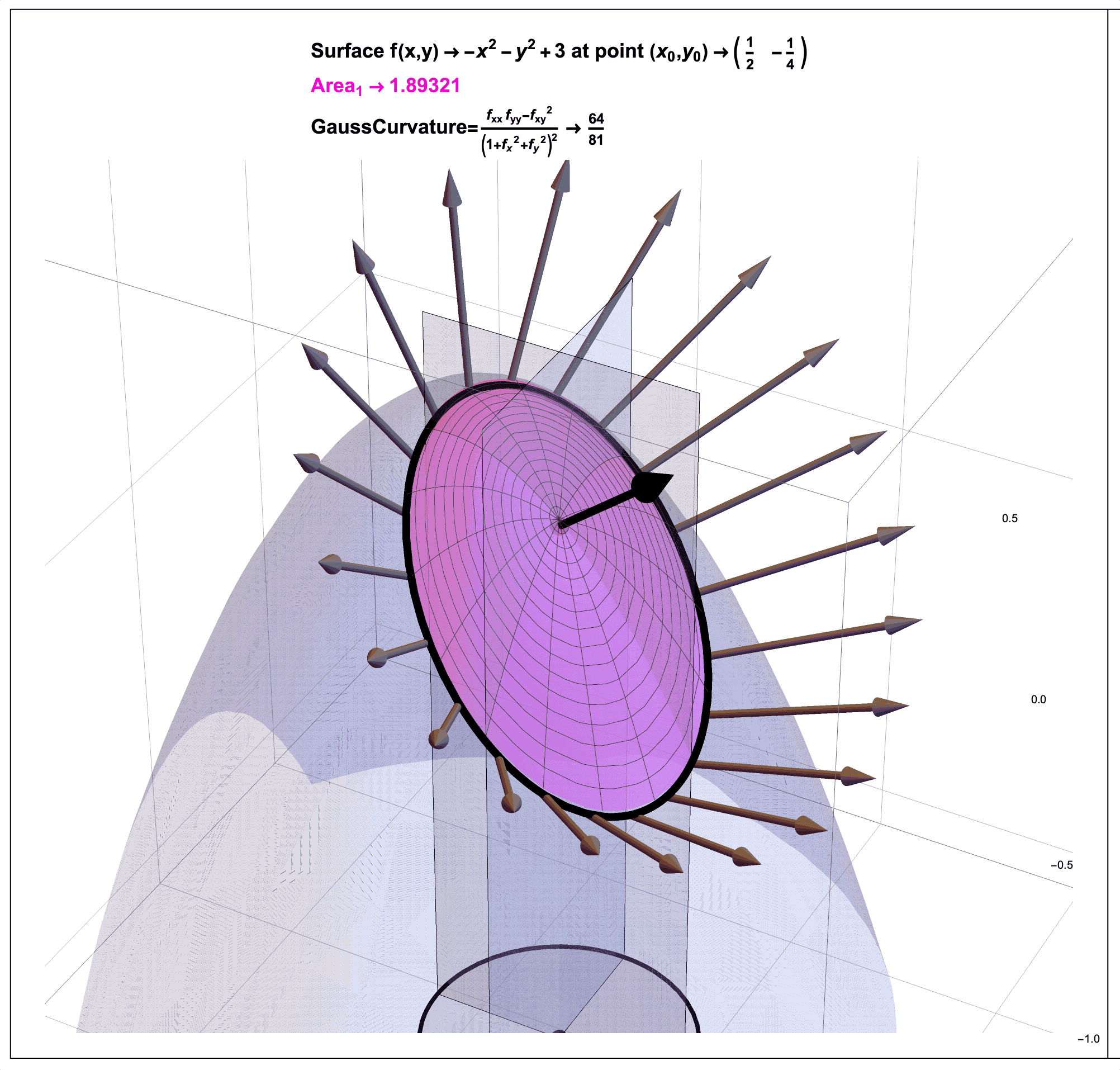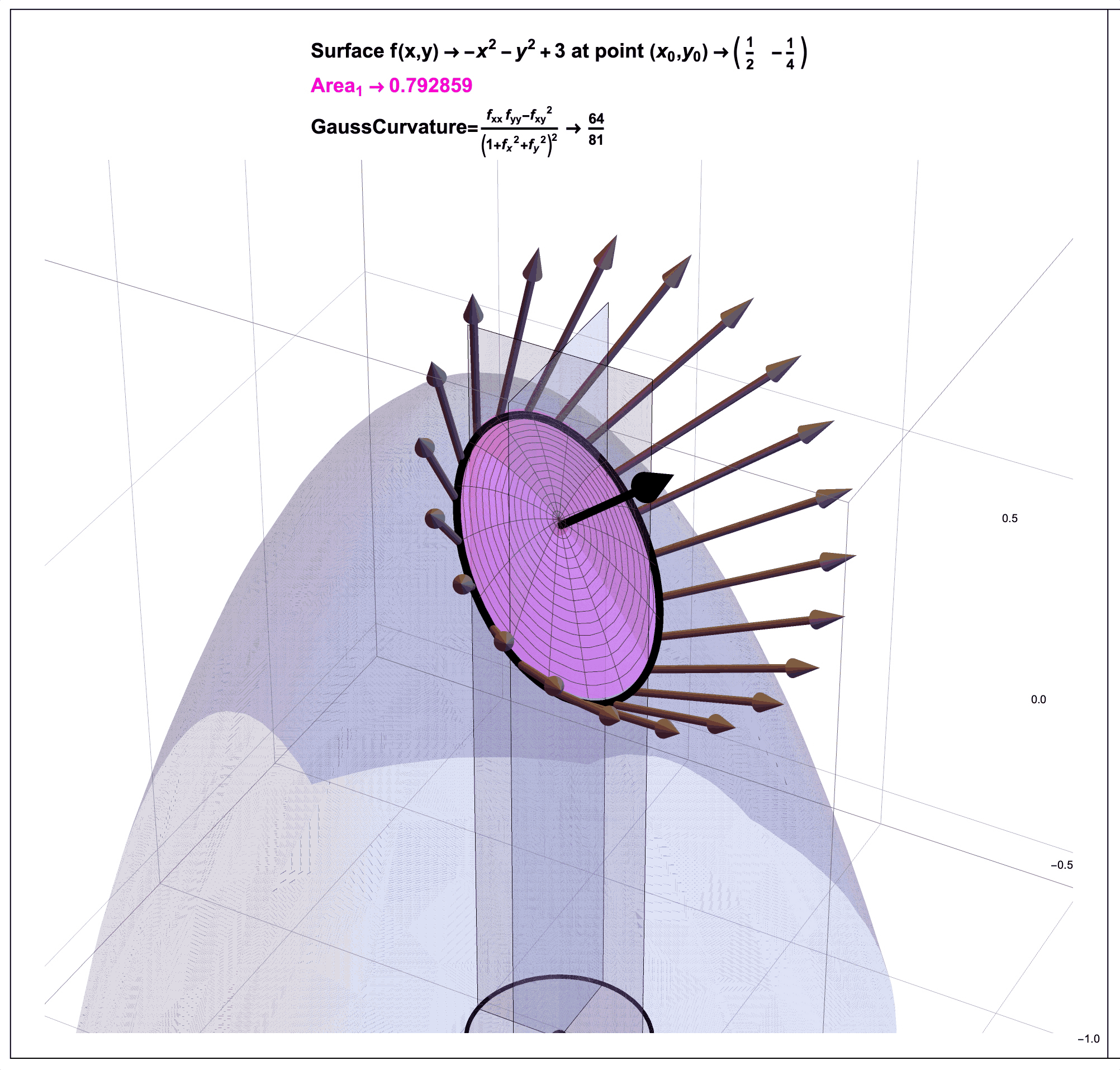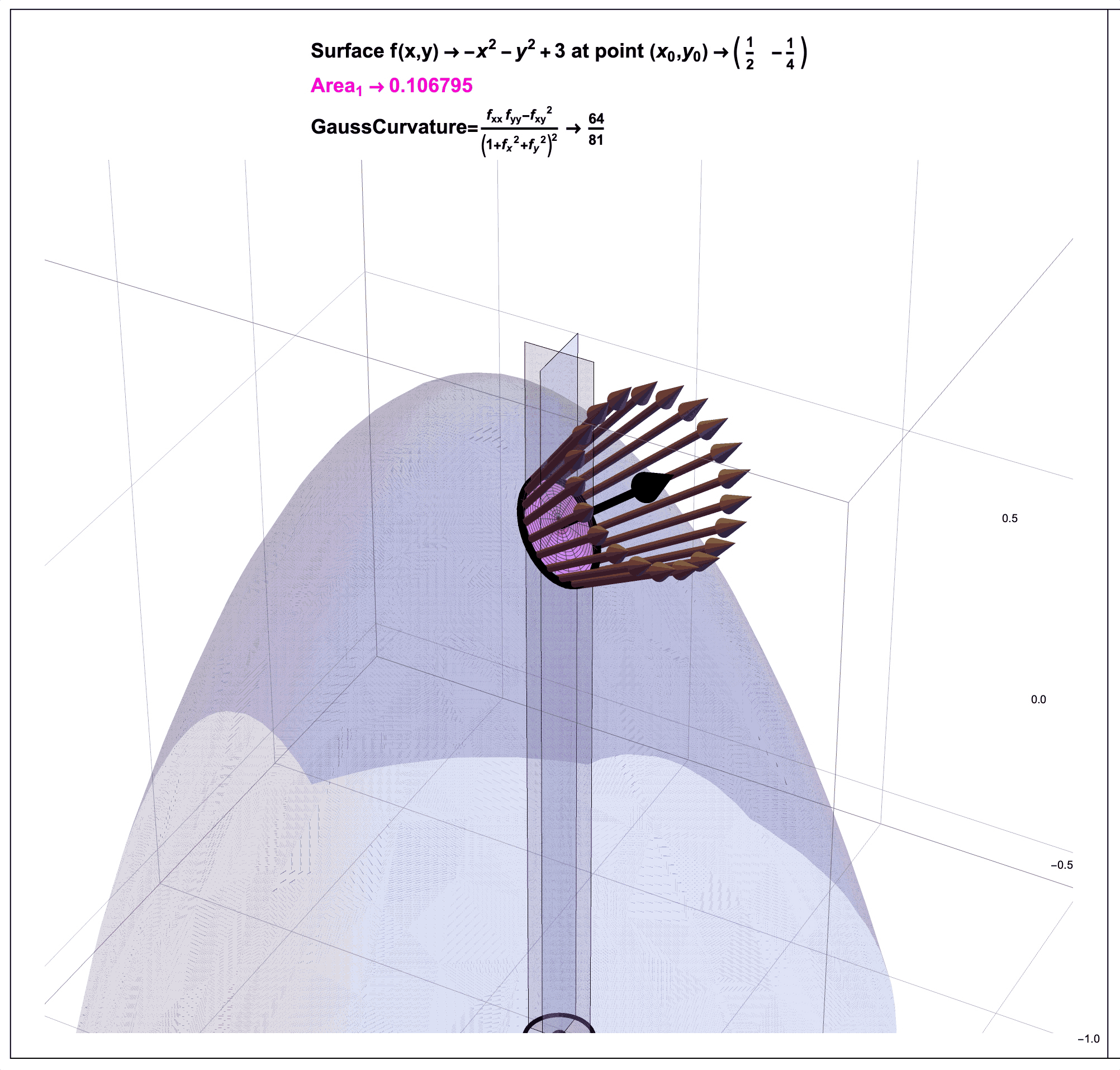

Figure 4: Gauss Curvature Illustration: A Ratio of Areas
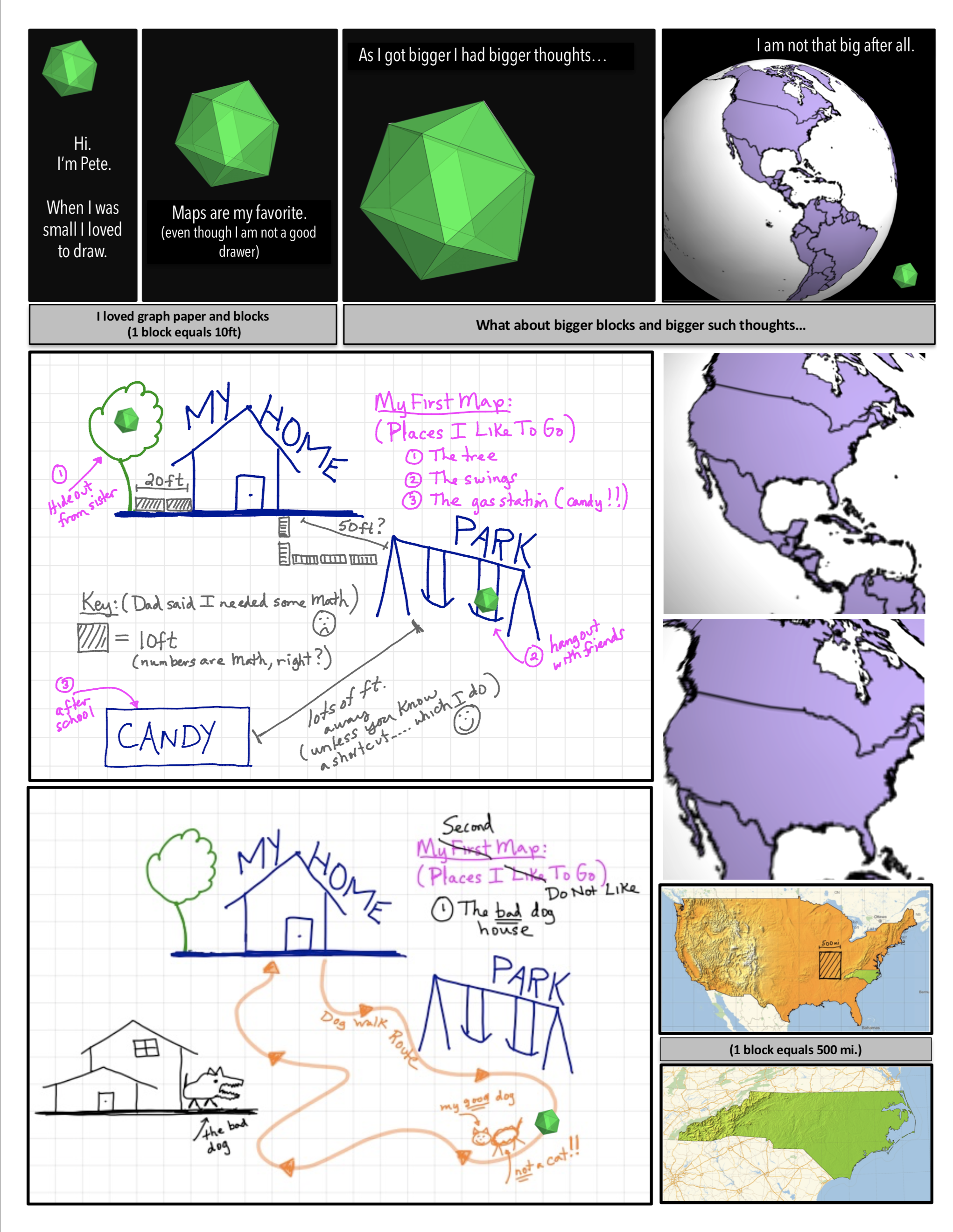
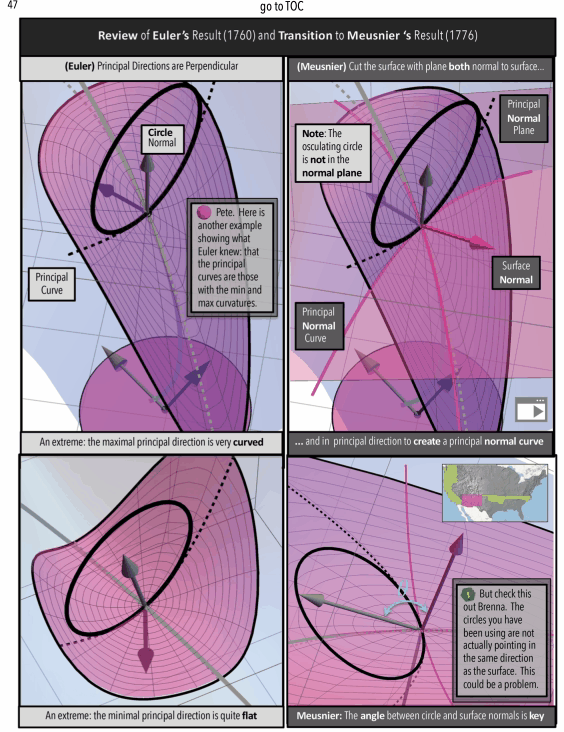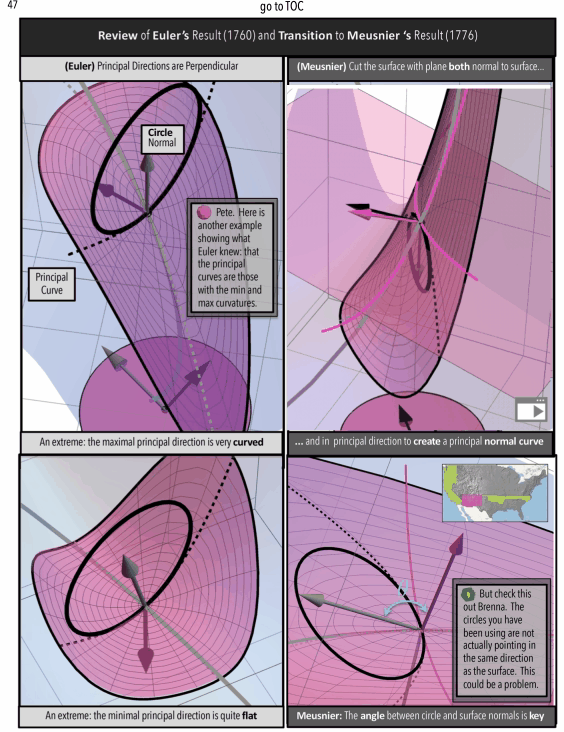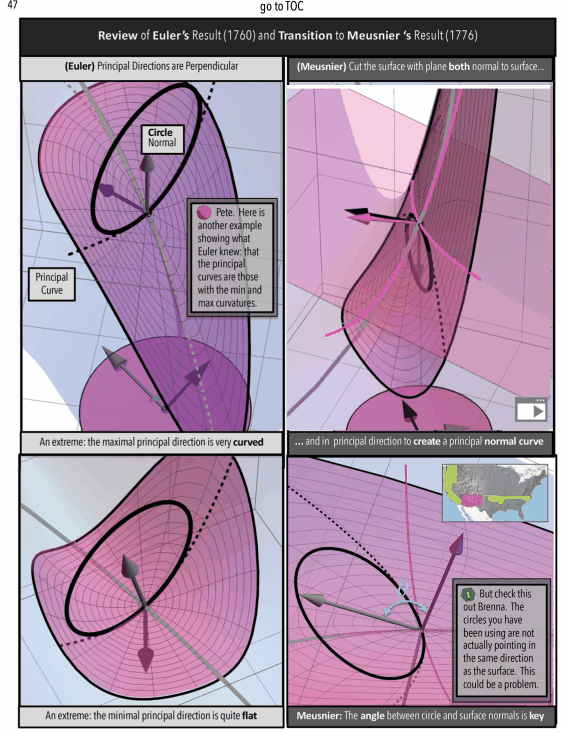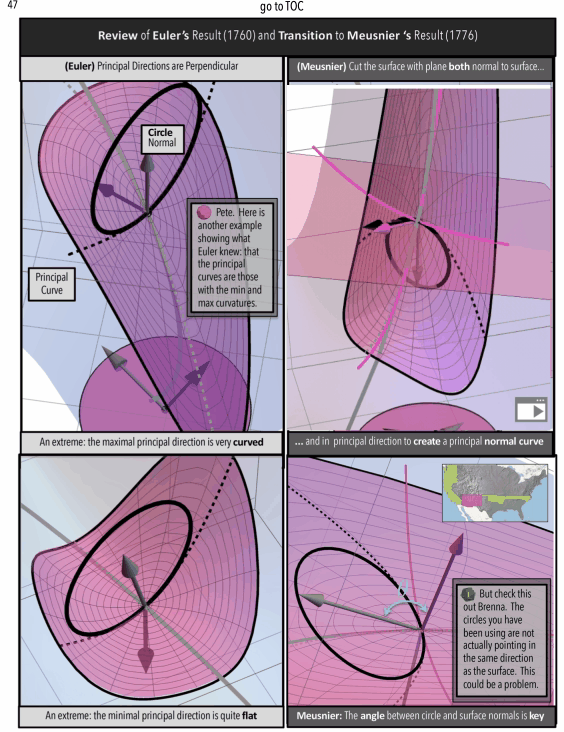

Figure 5: Gauss Curvature as an Animated Graphic Novel: Find “A Curvature Story” on Apple Books (shorturl.at/EGOXY)







![Screenshots from tensorAddOns[RiemannCurvatureOnSurface] and tensorAddOns[SurfaceData] which Shows how the Riemann Curvature Defines the Gauss Curvature.](Images/MapleConf2022-Motivation-7-Annotated.png)
Figure 6: Screenshots from tensorAddOns[RiemannCurvatureOnSurface] and tensorAddOns[SurfaceData] which Shows how the Riemann Curvature Defines the Gauss Curvature.
A Comparison: The Packages tensorAddOns and Physics


















Figure 7: A tensorAddOns vs. Physics package Comparison of the Computation of the Riemann Curvature Tensor of the Schwarzschild Metric
The Question: An Example Only tensorAddOns Can Do?










Figure 8: tensorAddOns Computes the Riemann and Ricci Curvature Tensors in an Orthonormal, Anholonomic Frame
More Info: Check out our blog unconcisemath.com
- Currently 36 functions in the package tensorAddOnsTools and tensorAddOnsComps.
- Many documentation examples have been written that are in need of testing and demonstration.


Figure 9: For more technical details, see the post tensorAddOns on our blog unconcisemath.com by jason M. Osborne.