A Pattern Language and Storytime
How A Pattern Language has informed the design and organization of my current approach to writing about mathematics
Last Updated: Sunday, October 02, 2022 - 15:23:22.
A Curvature Story (available on Apple Books) has benefited in design and organization from my reading of the book A Pattern Language: Towns, Buildings, Construction by Christopher Alexander, Sara Ishikawa, Murray Silverstein. Oxford University Press, 1977.

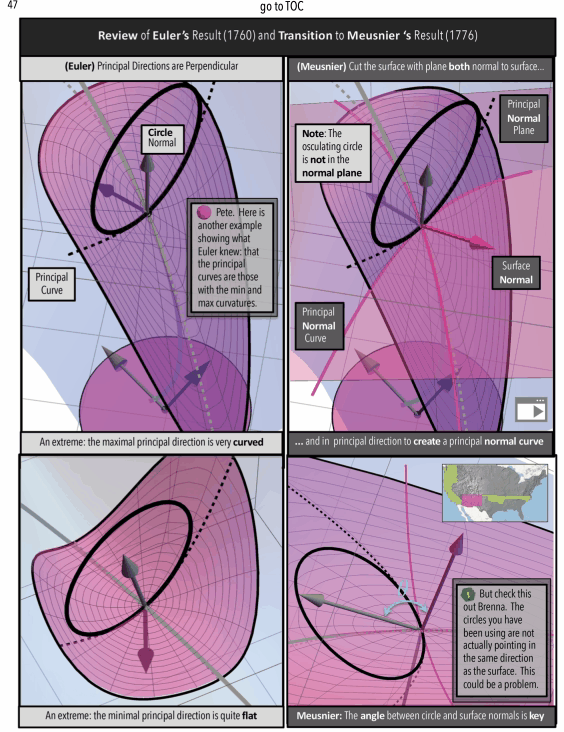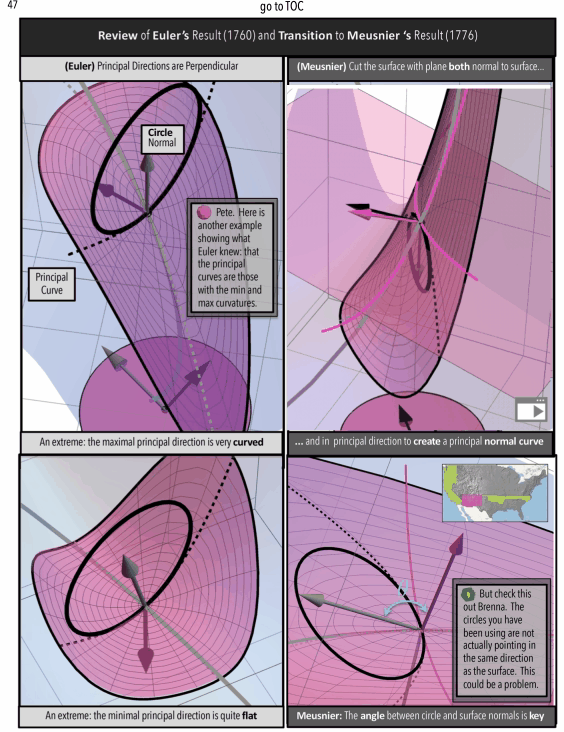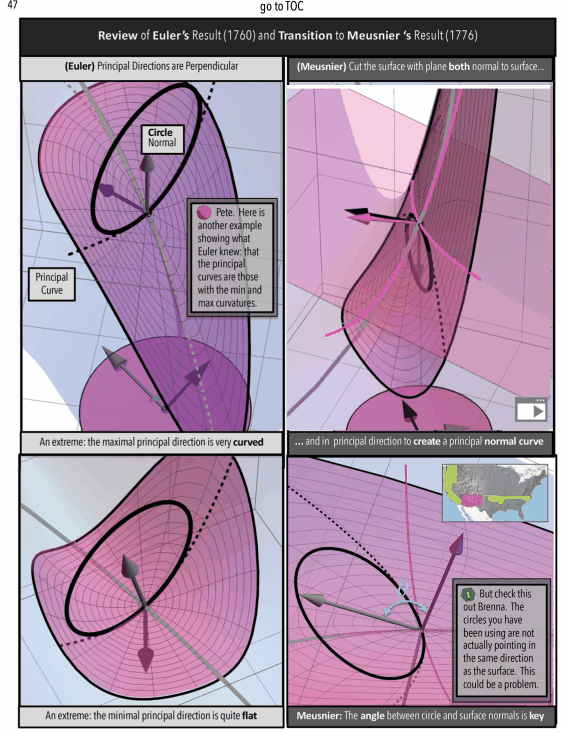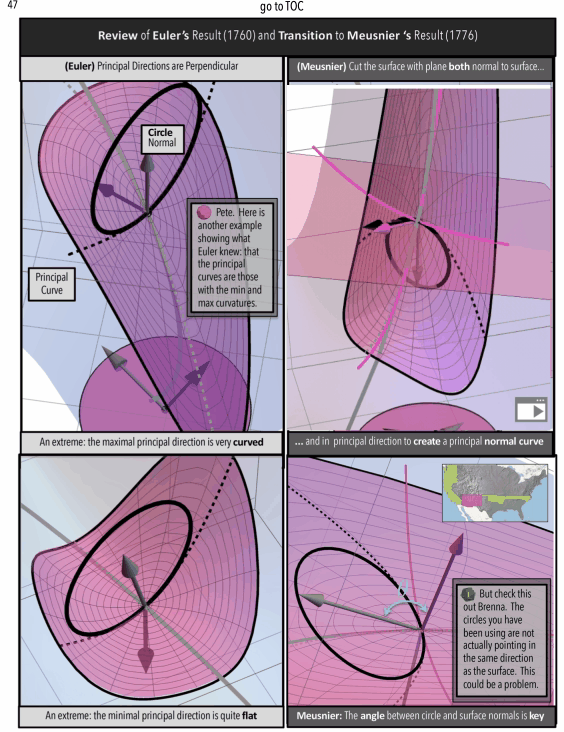

Figure 1: A Curvature Story Excerpts. (top/left) Title Page (middle 1) Meet Pete-A Character in the Story (middle 2) Math In Animated Graphic Novel Form (bottom/right) Math In Traditional Form: The Professor’s Indecipherable Notes (See More Screenshots Here)



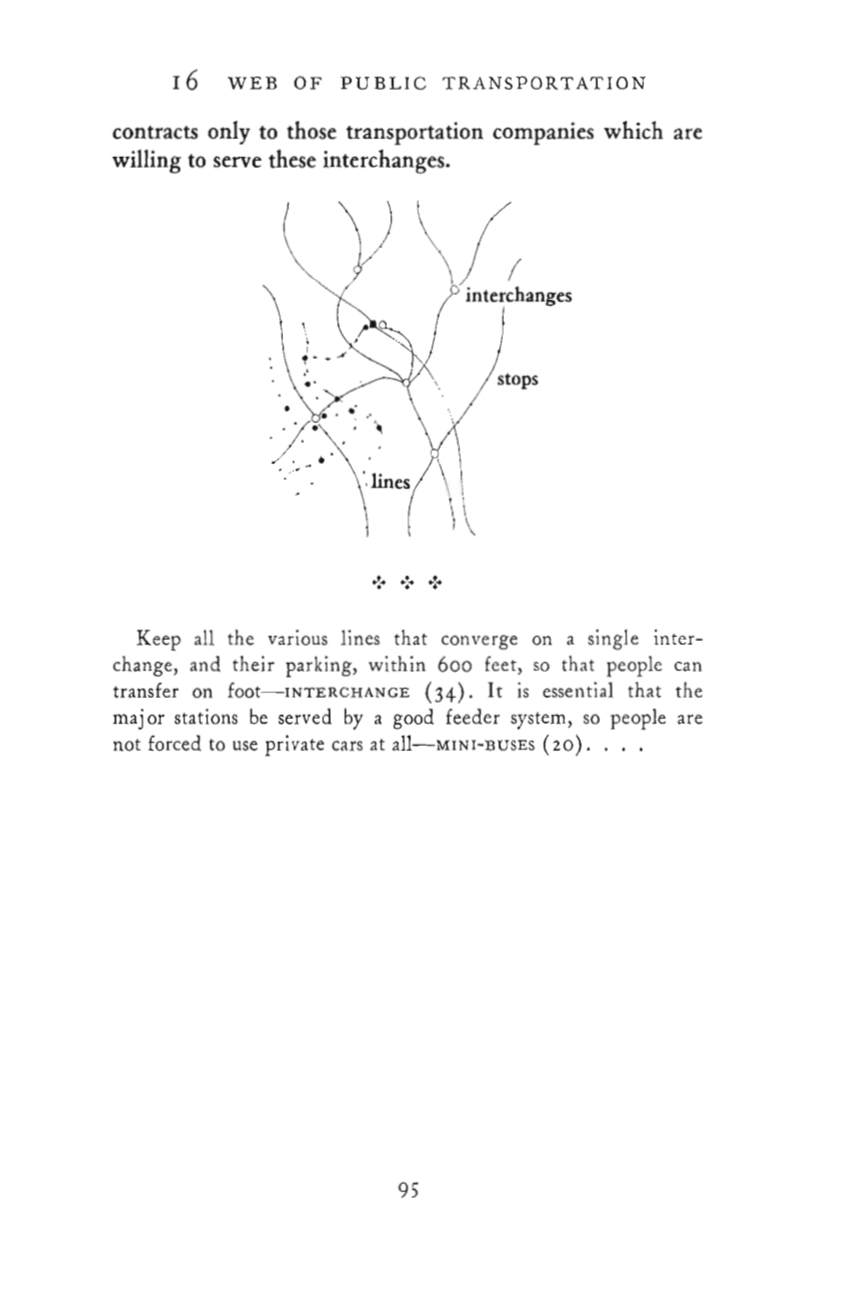
Figure 2: A Pattern Language Samples. (top/left) Title Page (middle 1) Contents (middle 2) Pattern 16: Web of Public Transportation is “Fed” by Prior Pattern 3: City Country Fingers and Pattern 11: Local Transport Areas (bottom/right) To “Delve Deeper” Into Achieving Pattern 16 Then See Pattern 20: Minibuses and Pattern 34: Interchanges
A Pattern Language: In Abstraction
To my reading and understanding, “A Pattern Language” is ostensibly about the authors views on the interconnection between towns and cities (on a large, monolithic scale) as a collection of buildings and infrastructure (on a more focused, medium scale) where design, construction, and usability based on the human experience (on the individual, or small scale) should be of primary consideration. The authors convey their thoughts about the physically constructed world (brick and mortar, building, roads, and in-between space, etc.) and its relationship to a societies needs of this space (work and neighborhood communities, public and shared space, home, etc.) using what the authors called “A Pattern Language”. In essence, a “Pattern Language” is a “network” of fundamental ideas or “invariants” called the Patterns whose relationships and interconnections comprise the “Language” that is written, for convenience, as a “straight, linear sequence”.
According to the authors of the Pattern Language, “What is most important about this sequence, is that it is based on connections between patterns. Each pattern is connected to certain “larger” patterns which come above it in the language; and to certain “smaller” patterns which come below it in the language. The pattern helps to complete those larger patterns which are “above” it, and is itself completed by those smaller patterns which are “below” it”.
A Pattern Language: A Mystery Novel Analogy
To think about the abstract ideas and terminology of A Pattern Language in context, you might consider your favorite book. From a publishers point of view , and for the readers convenience, it helps to have a book that is bound together as a collection of pages-one page following the other; this book is the “straight, linear sequence” of the Language. But any book worth reading has interesting and unique characters or ideas; these characters comprise the “Patterns” of the Language. It is likely that your chosen book is not your favorite simply because you liked one particular character or one interesting idea, but rather it was how these characters came to know and interact with each other that made it your favorite; it is these relationships that make the “Language” and it is this language that gives the individual patterns or characters in isolation their depth and importance in aggregation as a “network”.
In the context of your favorite book analogy, the Pattern Language authors could essentially be giving a blueprint and a how-to for writing a mystery novel:
A “large pattern” could be the Pattern::Location where the books mystery will be happening. Let’s say the book is set in the city of “London”. A pattern “above” this could be the Pattern::Country given by “England” (as opposed to the state “Arkansas”). The pattern “England” is completed by the pattern “London” because it gives us a better, more complete visual of being in a crowded city with double–decker buses instead of narrow country lanes and sheep or a two-lane highway and road-kill armadillos.
A “smaller” pattern “below” Pattern::Location is Pattern::Characters which inhabit this location, say, the police officer “Sahid” and bystander “Brittany”. It is the “Language” which, in each characters chapter, explores their lives in the city of London, England with hints about how their separate stories might eventually become entangled.
Because the book being described is a mystery, we understand there is likely a larger story to unfold. It is up to the subsequent chapters/Patterns further and further “below” the Pattern::Location and Pattern::Characters to complete the story. Only by the end of the book (by the time the Language has fully explored the relationships) will we understand the complete story; maybe that Sahid, before he was a police officer in London, grew up in the same neighborhood in Dehli as Brittany’s husband, Raj, who, we come to find, was murdered to intimidate Britanny (a London lawyer) into not prosectuting a case involving money laundering…etc…etc.
A Pattern Language: Deeper Into The Abstract Organizational Structure
The mystery book analogy does not quite do justice to the organizational structure of the Pattern Language, since a mystery is likely meant to and probably will be read from page 1 to 2 to 3, and up until the end in an ascending order.
A unique feature of the Pattern Language is the pattern directly above and directly below any other pattern in the sequence will be those that the authors deem important to establishing context and detail, but which might not directly relate to the readers own interests. A reader of the Pattern Language interested in exploring a particular, self-selected pattern in the middle of the author’s story might need to move many patterns ahead or behind to trace the pattern-of-interest to its origin or conclusion. In other words, in the Pattern Language, a reader can, according to their interests, follow a sub-story in a way that might differ from the author’s original intent.
A Pattern Language: A Specific Example
My own particular interest in the Pattern Language began with a particular sub-story of a sub-story within the overall network of building and construction, namely that of constructing a very specific building called a “Home” which sits in the larger context of a city or town or community. Giving a detailed example of the Pattern Language in use will hopefully illustrate my over-arching interests in this method of organization for the conveyance of abstract mathematical ideas.
In the “straight linear sequence” of ideas that is the book called “A Pattern Language”, one comes to a section called “Buildings” linearly organized by the authors as
Pattern 95::Building Complex
Pattern 96::Number of Stories
Pattern 97::Shielded Parking
Pattern 98::Circulation Realms
Pattern 99::Main Building, etc. etc.
These patterns are aptly chosen because the reader can easily guess their content and organization just by each pattern’s title and relative location to other patterns. That is, a home might need to been part of a “Building Complex” so one should probably start in that section. But likely a person or family will need just one building to live in, and therefore, from context, a person building a home could eventually find their way into “Main Building” which is at a more refined scale lower down in the building process. Indeed, after reading “Pattern 95::Building Complex” we find the connecting patterns (the language) in the form of a succinct summary:
- “Arrange the buildings in the complex to form realms of movement-Circulation Realms (98); build one building from the collection as a main building-the natural center of the site-Main Building (99)…”
It is interesting to me to note that these two seemingly important patterns in making a good Building Complex (95) are a couple of patterns ahead (98) and (99) in the authors linear sequence. Continuing the summary we find other patterns of interest:
- “Place individual buildings where the land is least beautiful, least healthy-Site Repar (104); and put them to the north of their respective open space to keep the gardens sunny- South Facing Outdoors (105); subdivide them further, into narrow wings, no more than 25 or 30 feet across- Wings of Light (107). For details of construction, start with Structure Follows Social Spaces (205)….”
From this simple summary of pattern names we can begin to see the authors intent; to build a building with access to natural light and with the regards to the eventual human uses of the space. Continuing, from Pattern 99::Main Building we learn that Pattern 129::Common Areas At The Heart is also of importance and from Pattern 105::South Facing Outdoors we learn that Pattern 107::Wings of Light is again of importance and so to is Pattern 128: Indoor Sunlight. In this way anyone can easily skip around in the overall linear sequence to explore patterns that fit the goals and constraints of designing their own particular home. In fact, since each pattern is written in such a concise and self-contained way it is possible, in my opinion, to pick the book up at any point and begin reading and learning something valuable from it.
A Pattern Language: Extension to Mathematical Writing
It is the fragmented and yet connected readability of A Pattern Language that strikes me as being extensible to the writings of mathematics. In doing so one might consider:
Identify patterns, and compose these patterns as short, self-contained sections in a sequence-independent way.
While important, mathematical facts might not matter perhaps as much as the connections between these facts.
The connections form the language and it is these connections that might interest students. It is these connections which interest mathematicians about mathematics.
Compose the patterns with the connections in mind.
Many patterns related to our physical, lived-in world have a name that conveys a learned meaning. Mathematical patterns might need a “story” to give context and meaning to these abstract ideas.
A Pattern Language: As a Di-Graph
For the sake of completeness, reading the Pattern Language with a particular focus on building a home led to the 51-Patterns (seen in Figure 3) below as a starting point for future conversations between myself and those who might become involved in the project.

Figure 3: The 51 Selected Patterns To Be Viewed As A Network
It became an interesting idea to me to visualize the “language” or “network” resulting from these patterns. What stories or patterns within the patterns would result? To a mathematician, a “Pattern” is a “Node in a Graph” and the “Connections to Smaller or Larger Patterns” are “the Directed Edges of the Graph” and the “Pattern Language” becomes a “Di-Graph” or a graphical representation of the Pattern Language.
What we are seeing in Figure and Figure are the early stages of the Pattern Language developing. From a thoughtful identification and intelligent naming of the patterns to a careful consideration of the connections between these patterns, we can begin to understand the home-building story:
- To build a home for a small family (76) you need to carefully consider details of and create space for both the adults (136) and the children (137) in this home. On a larger scale, one will need to consider the physical layout (129) and privacy concerns (127) to accomodate these humans needs. And on the story goes to show that, despite its excellent physical layout concerning its inhabitants spacial needs, without natural light (105) obtained via careful site location (104) a home will probably not function very well and might affect sleep (138). To encourage general well-being consider bringing light (128) into the space (236) and into the kitchen (199). On the story goes to increased complexity.
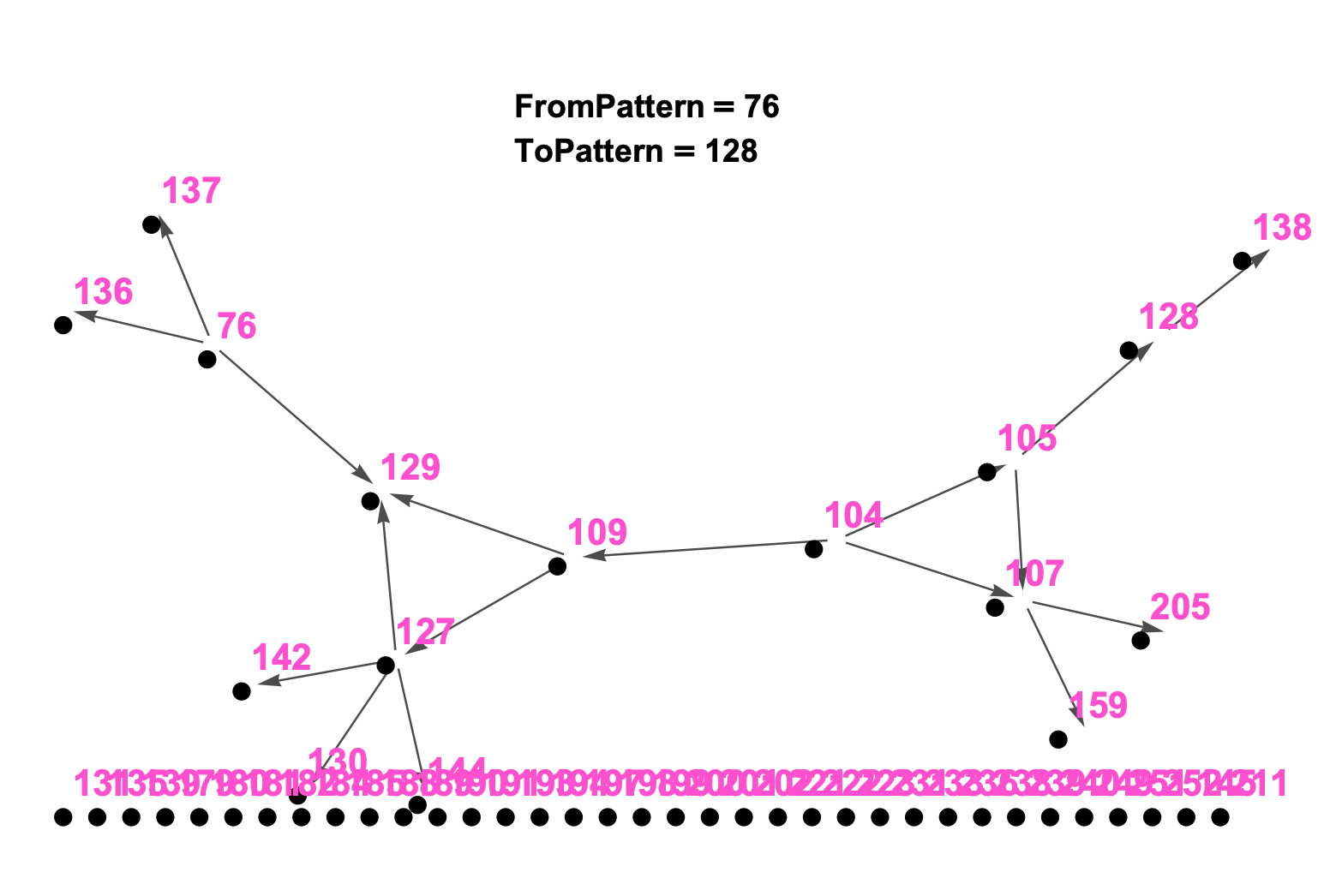
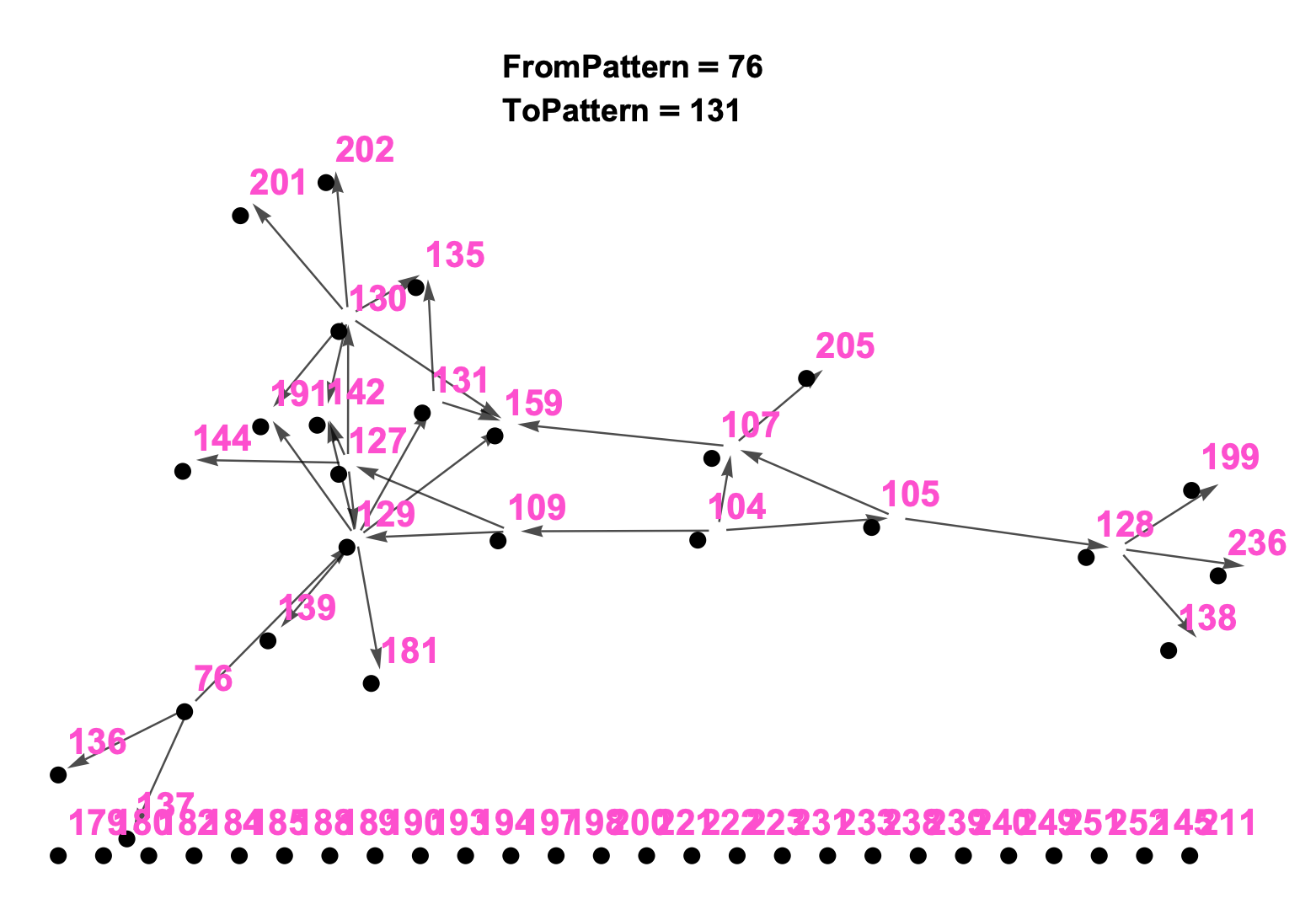
Figure 4: (top/left) The 51 Patterns In Early Stage of Network-ification ** (botton/right) 51 Patterns In Middle Stage of Network-ification
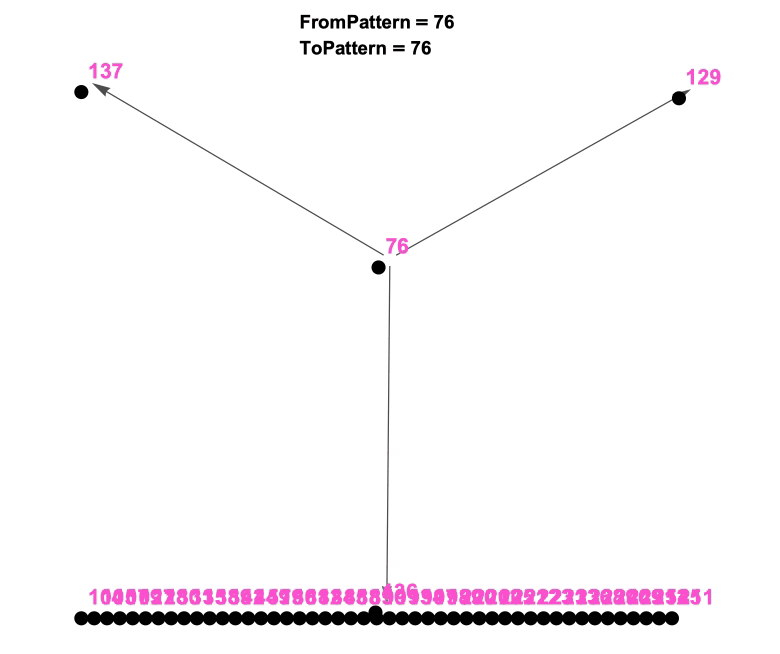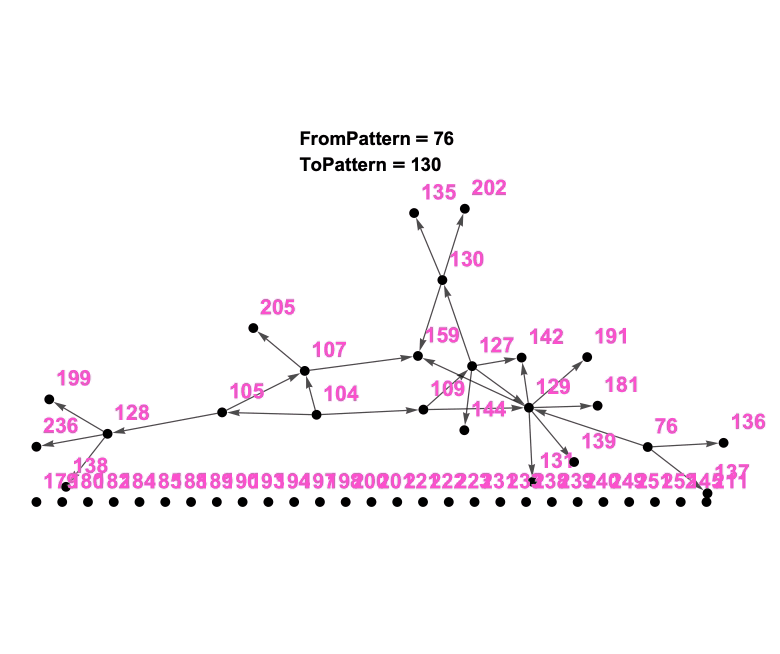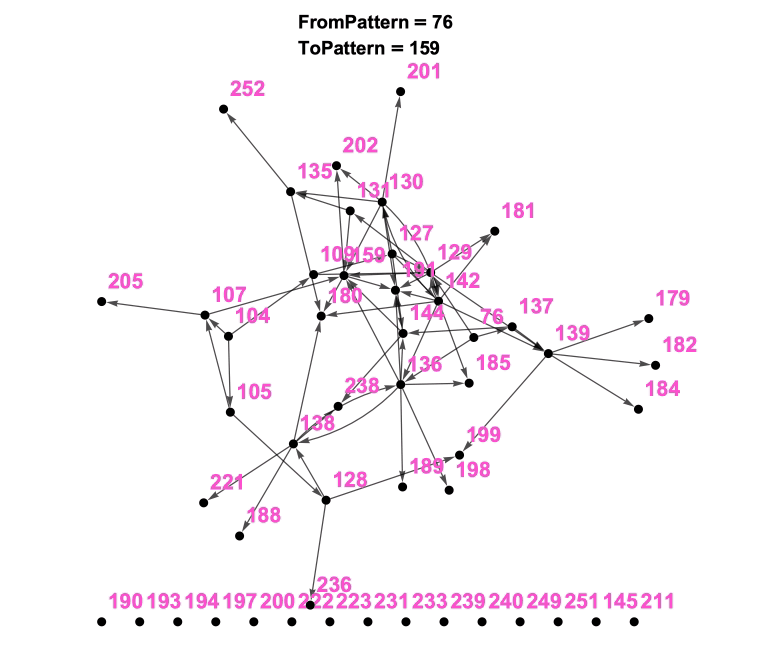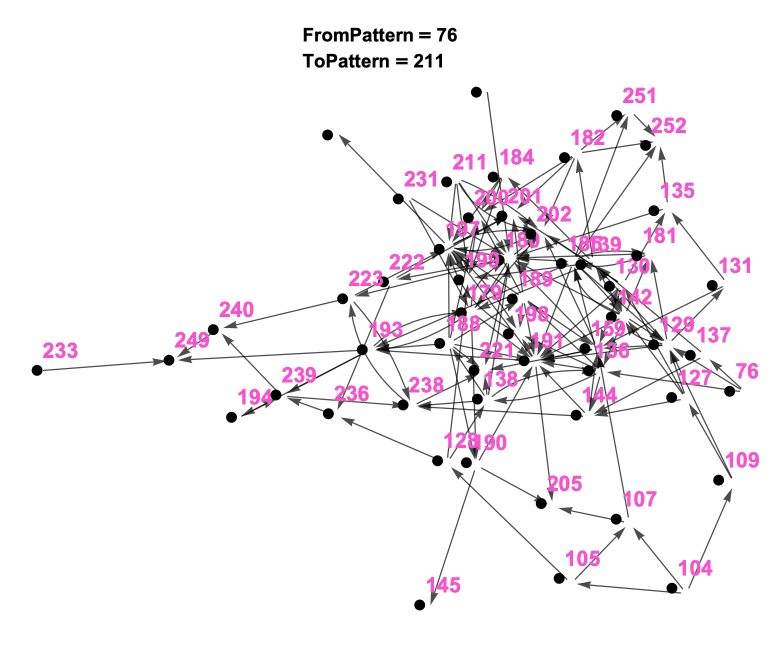
Figure 5: The 51 Patterns As An Animated Network
From A Pattern Language To A Curvature Story
To a mathematician, the subject of “curvatue and differential geometry” can be seen as a “straight-linear, sequence” of definitions , ideas, and results, but non-mathematicians trying to understand and connect these ideas into a network might find some other organizational structure necessary. What form this organization might take is particularly interesting to me. As explored in A Curvature Story (available on Apple Books), we follow the semi-contained chapters in the story of two characters tracking the historical origins of the mathematical concept of curvature.